Saymanın Temel Kuralları:
Bir çokluğu saymak için üç yöntem uygulanır. Bunlar: Eşleme – toplama ve çarpma yöntemleridir.
A) Eşleme Yöntemi:
Saymak istediğimiz çokluğun elemanları ile 1 den başlayan doğal sayıları 1-1 eşlersiniz. En son eşlenen sayı o çokluğun sayısını verir. Örneğin bir grupta bulunan öğrencileri saymak eşleme yöntemi ile saymaktır.
B) Toplam Yöntemi:
Daha önce ayrı ayrı sayılan kümelerin eleman sayılarını toplayarak, bunların tümünden oluşan kümenin eleman sayısını bulma yöntemidir. Örneğin cebimizdeki para çokluğunu bulmak için üzerilerinde yazılı miktarların toplamını alırsınız.
C) Çarpma Yöntemi:
Sayılması istenen çokluk ayrı ayrı gruplardan oluşuyorsa, her gruptaki çoklukların sayıları ile grup sayısının çarpımları alınır..Sayılması istenen miktar bulunmuş olur.
Bu yöntemle çokluk sayısını bulmaya çarpma yöntemi denir.
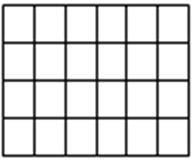
Örneğin yukarıdaki dikdörtgende bulunan karelerin sayısını bulalım. Burada 6 sütun ve her sütunda 4 kare olduğundan kare sayısını bulmak için bunlar çarpılır. 6 . 4 = 24 bulunur. Bu yolla kare sayısı bulma yöntemi çarpma kuralını kullanma yöntemidir.
Bu yöntemle çözülebilen problemleri inceleyelim.
ÖRNEK:
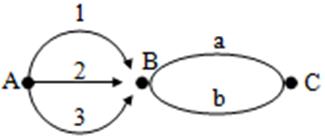
A dan B ye 3
değişik yol B den
C ye iki değişik
yol vardır.
A dan (B den geçme koşulu ile) C ye kaç değişik yolla gidilebilir?
ÇÖZÜM:
Yollar
olmak üzere 6 yol bulunur.
Çarpma yöntemi ile daha çabuk 3 . 2 = 6 olarak bulunur.
ÖRNEK:
KONYA kelimesindeki harflerle beş harfli anlamlı yada anlamsız kaç sözcük yazılabilir?
ÇÖZÜM:
Beş harfi yandaki
1: Numaraya 5 değişik harf yazılabilir.
2: Numaraya 4 değişik harf yazılabilir.
(Çünkü bir harf 1 numaraya yazılmıştır.)
3: Numaraya 3 değişik harf yazılabilir.
4: Numaraya 2 değişik harf yazılabilir.
5: Numaraya ise 1 harf kalır. Yazıla-bilecek sözcük sayısı,
çarpma yöntemi gereğince 5 . 4 . 3 . 2 . 1 = 120 olarak bulunur.
ÖRNEK:
İki torbanın birinde siyah ve diğerinde beyaz ve üzerlerinde 1,2,3,4,5 numaraları yazılı 5 er bilye vardır. Bu torbaların her birinden birer bilye çekilerek ikililer elde ediliyor. Bu ikililerin sayısı kaçtır?
ÇÖZÜM:
Çarpma yöntemi ile 5.5 = 25 ikili bulunur.
ÖRNEK:
kümesinin elemanlarını kullanarak 300 den büyük üç basamaklı kaç tane sayı yazabiliriz. (Bir kez kullandığınız rakamı bir daha kullanabilirsiniz)ÇÖZÜM:
Üç basamaklı sayının yüzler basamağına ancak 3, 4, 5 rakamlarından biri gelir. Diğer basamaklara ise 5 rakamdan (bilgi yelpazesi.net) biri getirilebilir.
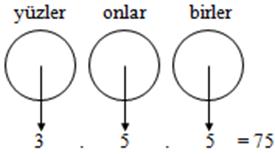
Çarpma yöntemi ile 3.5.5 = 75 sayı yazılabilir.
ÖRNEK:
kümesinin elemanları ile rakamlar tekrarsız ve 300 den büyük üç basamaklı kaç sayı yazabilirsiniz.
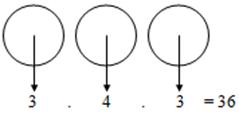
ÇÖZÜM:
Yüzler basamağına 3 değişik rakam onlar basamağına (yüzler basamağına bir rakam yazıldığı için) 4 değişik rakam ve birler basamağına da 3 değişik rakam yazılabilir. Çarpma yöntemi gereği bu değişik değerler çarpılır.
Bu hesapları daha çabuk yapabilmek için (faktöriyel) hesapları kullanılır.
Faktöriyel hesapları hatırlayalım.
Tanım: 1, 2, 3, 4........n (1 den n e kadar doğal sayıların çarpımı n nin yanına bir ünlem işareti konularak gösterilir ve n faktöryel diye okunur.)
1.2.3.4.5........n = n !
tanıma uymayan 0 ! ve 1 ! gösterimleri kullanılabilir ve değerleri 1 dir. 0! = 1; 1! = 1 dir.
Faktöryel Hesapları
n(n-1)(n-2) = 20n.(n+1) den
7(n2-3 n+2) = 20(n+1)
7n2 – 41n – 6 = 0 denklemi bulunur.
(n = - olamaz.)
ÖRNEK:
(n+!)[n.n! + (2n-1).(n-1)! + (n-1).(n-2)!]
çarpımının sonucu nedir?
ÇÖZÜM:
(n+1)[ n.n! + (2n-1).(n-1)! + (n-1).(n-2)!] =
(n+1)[ n.n! + (n-1).(2n-1) . (n-1)!+(n-1)!] =
(n+1) [(n-1)! . (n2 + 2n – 1 + 1)]
= (n+1) (n-1)! . n(n+2)
= (n-1)! n.(n+1)(n+2) = (n+2)! bulunur.
