01-02-2016 Saat: 14:12
ONDALIK SAYI OLUŞTURMA
Ondalık sayı oluşturmanın iki yolu vardır:
Birinci yol paydayı 10, 100, 1000, 10 000 ... gibi, 10 un kuvveti olan sayılara genişletmektir.
Örneğin ;
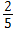 kesrinde paydayı 10 yapabilmek için kesri 2 ile genişletiriz.
kesrinde paydayı 10 yapabilmek için kesri 2 ile genişletiriz.
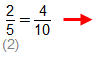 Bu kesrin okunuşu “onda dört” tür.
Bu kesrin okunuşu “onda dört” tür.
Ondalık gösterimi 0,4 tür.
Ondalık sayının okunuşu “sıfır tam onda dört” tür.
İkinci yol payı paydaya böleriz.
2 ÷ 5 = 0,4 tür.
DEVİRLİ ONDALIK GÖSTERİM
Bazı kesirlerin paydaları 10 un kuvvetine çevrilemez.
Örneğin 1/3 gibi.
Veya bazı kesirlerde payı paydaya bölerek ondalık gösterim elde etmek istediğimizde bölme işlemi sonlanamaz, hep devam eder.
1 ÷ 3 = 0,3333333 .....
Bu tür sayılara devirli ondalık sayı denir. Devirli ondalık sayılarda virgülden sonra hep tekrar eden sayı devreden sayıdır ve gösterimi farklıdır. Devreden sayının üstü çizilerek gösterilir.
Örnekler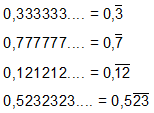
ONDALIK SAYILARI ÇÖZÜMLEME
Öncelikle ondalık sayıyı tanıyalım.
Ondalık sayılar tam kısım ve ondalık kısım olmak üzere iki bölümden oluşur.
Aşağıdaki tabloda 43,607 ondalık sayısının basamak adları ve basamak değerleri gösterilmiştir. İnceleyiniz. 43,607 ondalık sayısının çözümlenişi ise;
43,607 ondalık sayısının çözümlenişi ise;
43,607 = (4 x 10) + (3 x 1) + (6 x 0,1) + (0 x 0,01) + (7 x 0,001) şeklindedir.
ONDALIK SAYILARI YUVARLAMA
Yuvarlama yapılacak basamağın sağındaki ilk rakam incelenir. Bu rakam 5 veya 5’ten büyükse yuvarlama yapılacak basamaktaki rakama 1 eklenir, sağındaki diğer rakamlar atılır.
Bu rakam 5’ten küçükse yuvarlama yapılacak rakam değişmez, sağındaki rakamlar atılır.
Örnek : 52,137 ondalık sayısını yüzde birler basamağına yuvarlayalım.
Yüzde birler basamağının sağındaki 7 sayısı 5 ten büyük olduğu için yüzde birler basamağı
1 artar. Yüzde birler basamağının sağında kalan 7 ise yazılmaz.
 Örnek : 17,346 ondalık sayısını onda birler basamağına yuvarlayalım.
Örnek : 17,346 ondalık sayısını onda birler basamağına yuvarlayalım.
Onda birler basmağının sağındaki 4 sayısı 5 ten küçük olduğu için, onda birler basamağındaki sayı aynen kalır. Onda birler basamağının sağındaki rakamlar ise yazılmaz.
Örnek : 13,572 ondalık sayısını birler basamağına yuvarlayalım.
Birler basamağının sağındaki rakam 5 e eşit olduğu için, birler basamağı 1 artar. Birler basamağının sağındaki rakamlar ise yazılmaz.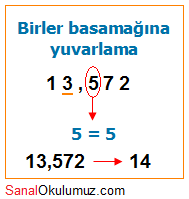
ONDALIK SAYILARDA ÇARPMA İŞLEMİ
Örnekte de görüldüğü gibi virgül yokmuş gibi çarpma yapılır. Fakat dikkat etmemiz gereken bir kural var. Çarpanların virgülden sonra toplam kaç tane basamağı varsa çarpımda sağdan sola o kadar basamak virgül ile ayrılır.
ONDALIK SAYILARI KISA YOLDAN 10, 100, 1000 İLE ÇARPMA
Bir ondalık sayıyı 10 ile çarptığımızda virgül bir basamak sağa atlar.
100 ile çarptığımızda virgül iki basamak sağa atlar.
1000 ile çarptığımızda virgül üç basamak sağa atlar.
Örnekler:
0,512 x 100 = 51,2
12,135 x 10 = 121,35
15,1 x 1000 = 15100 (basamak yoksa sıfır ile basamak oluşturulur.)
ONDALIK SAYILARDA BÖLME İŞLEMİ
Bölme işleminde ondalık sayıları virgülden kurtarmak gerekir. Bunun için 10, 100, 1000 .... gibi 10 un kuvvetlerinden yeterli olan ile sayılar kısayoldan çarpılır.
Örnek : 2,4 ÷ 0,6 bölme işleminde sayıları virgülden kurtarmak için 10 ile kısayoldan çarpmak yeterlidir.
2,4 x 10 = 24 ve
0,6 x 10 = 6 olur.
Bölme işlemi böylece kolaylaşır.
24 ÷ 6 = 4 olur.
Örnek :0,3 ÷ 002 bölme işleminde ise sayıları 10 ile çarpmak yeterli değildir.
0,02 sayısını ancak 100 ile çarparsak virgülden kurtulur.
Bu durumda her iki sayıyı da 100 ile çarpmak zorundayız.
0,3 x 100 = 30 ve
0,02 x 100 = 2 dir.
Bölme işlemini yapalım.
30 ÷ 2 = 15 olur.
ONDALIK SAYILARI KISA YOLDAN 10, 100, 1000 İLE BÖLME
Bir ondalık sayıyı 10 ile böldüğümüzde virgül bir basamak sola atlar.
100 ile böldüğümüzde virgül iki basamak sola atlar.
1000 ile böldüğümüzde virgül üç basamak sola atlar.
Örnekler:
12,56 ÷ 10 = 1,256
345,3 ÷ 100 = 3,453
1,2 ÷ 1000 = 0,0012 (basamak yoksa sıfır ile basamak oluşturulur.)
Ondalık sayı oluşturmanın iki yolu vardır:
Birinci yol paydayı 10, 100, 1000, 10 000 ... gibi, 10 un kuvveti olan sayılara genişletmektir.
Örneğin ;
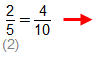 Bu kesrin okunuşu “onda dört” tür.
Bu kesrin okunuşu “onda dört” tür.Ondalık gösterimi 0,4 tür.
Ondalık sayının okunuşu “sıfır tam onda dört” tür.
İkinci yol payı paydaya böleriz.
2 ÷ 5 = 0,4 tür.
DEVİRLİ ONDALIK GÖSTERİM
Bazı kesirlerin paydaları 10 un kuvvetine çevrilemez.
Örneğin 1/3 gibi.
Veya bazı kesirlerde payı paydaya bölerek ondalık gösterim elde etmek istediğimizde bölme işlemi sonlanamaz, hep devam eder.
1 ÷ 3 = 0,3333333 .....
Bu tür sayılara devirli ondalık sayı denir. Devirli ondalık sayılarda virgülden sonra hep tekrar eden sayı devreden sayıdır ve gösterimi farklıdır. Devreden sayının üstü çizilerek gösterilir.
Örnekler
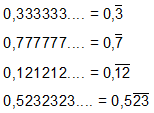
ONDALIK SAYILARI ÇÖZÜMLEME
Öncelikle ondalık sayıyı tanıyalım.
Ondalık sayılar tam kısım ve ondalık kısım olmak üzere iki bölümden oluşur.
Aşağıdaki tabloda 43,607 ondalık sayısının basamak adları ve basamak değerleri gösterilmiştir. İnceleyiniz.
 43,607 ondalık sayısının çözümlenişi ise;
43,607 ondalık sayısının çözümlenişi ise;43,607 = (4 x 10) + (3 x 1) + (6 x 0,1) + (0 x 0,01) + (7 x 0,001) şeklindedir.
ONDALIK SAYILARI YUVARLAMA
Yuvarlama yapılacak basamağın sağındaki ilk rakam incelenir. Bu rakam 5 veya 5’ten büyükse yuvarlama yapılacak basamaktaki rakama 1 eklenir, sağındaki diğer rakamlar atılır.
Bu rakam 5’ten küçükse yuvarlama yapılacak rakam değişmez, sağındaki rakamlar atılır.
Örnek : 52,137 ondalık sayısını yüzde birler basamağına yuvarlayalım.
Yüzde birler basamağının sağındaki 7 sayısı 5 ten büyük olduğu için yüzde birler basamağı
1 artar. Yüzde birler basamağının sağında kalan 7 ise yazılmaz.
 Örnek : 17,346 ondalık sayısını onda birler basamağına yuvarlayalım.
Örnek : 17,346 ondalık sayısını onda birler basamağına yuvarlayalım.Onda birler basmağının sağındaki 4 sayısı 5 ten küçük olduğu için, onda birler basamağındaki sayı aynen kalır. Onda birler basamağının sağındaki rakamlar ise yazılmaz.

Örnek : 13,572 ondalık sayısını birler basamağına yuvarlayalım.
Birler basamağının sağındaki rakam 5 e eşit olduğu için, birler basamağı 1 artar. Birler basamağının sağındaki rakamlar ise yazılmaz.

ONDALIK SAYILARDA ÇARPMA İŞLEMİ
Örnekte de görüldüğü gibi virgül yokmuş gibi çarpma yapılır. Fakat dikkat etmemiz gereken bir kural var. Çarpanların virgülden sonra toplam kaç tane basamağı varsa çarpımda sağdan sola o kadar basamak virgül ile ayrılır.
ONDALIK SAYILARI KISA YOLDAN 10, 100, 1000 İLE ÇARPMA
Bir ondalık sayıyı 10 ile çarptığımızda virgül bir basamak sağa atlar.
100 ile çarptığımızda virgül iki basamak sağa atlar.
1000 ile çarptığımızda virgül üç basamak sağa atlar.
Örnekler:
0,512 x 100 = 51,2
12,135 x 10 = 121,35
15,1 x 1000 = 15100 (basamak yoksa sıfır ile basamak oluşturulur.)
ONDALIK SAYILARDA BÖLME İŞLEMİ
Bölme işleminde ondalık sayıları virgülden kurtarmak gerekir. Bunun için 10, 100, 1000 .... gibi 10 un kuvvetlerinden yeterli olan ile sayılar kısayoldan çarpılır.
Örnek : 2,4 ÷ 0,6 bölme işleminde sayıları virgülden kurtarmak için 10 ile kısayoldan çarpmak yeterlidir.
2,4 x 10 = 24 ve
0,6 x 10 = 6 olur.
Bölme işlemi böylece kolaylaşır.
24 ÷ 6 = 4 olur.
Örnek :0,3 ÷ 002 bölme işleminde ise sayıları 10 ile çarpmak yeterli değildir.
0,02 sayısını ancak 100 ile çarparsak virgülden kurtulur.
Bu durumda her iki sayıyı da 100 ile çarpmak zorundayız.
0,3 x 100 = 30 ve
0,02 x 100 = 2 dir.
Bölme işlemini yapalım.
30 ÷ 2 = 15 olur.
ONDALIK SAYILARI KISA YOLDAN 10, 100, 1000 İLE BÖLME
Bir ondalık sayıyı 10 ile böldüğümüzde virgül bir basamak sola atlar.
100 ile böldüğümüzde virgül iki basamak sola atlar.
1000 ile böldüğümüzde virgül üç basamak sola atlar.
Örnekler:
12,56 ÷ 10 = 1,256
345,3 ÷ 100 = 3,453
1,2 ÷ 1000 = 0,0012 (basamak yoksa sıfır ile basamak oluşturulur.)
Denetleme Ekibi Lideri: 22-06-2018 - ....



